Your Proof by induction examples images are ready in this website. Proof by induction examples are a topic that is being searched for and liked by netizens now. You can Find and Download the Proof by induction examples files here. Download all free photos and vectors.
If you’re looking for proof by induction examples images information connected with to the proof by induction examples interest, you have come to the ideal site. Our site frequently gives you hints for viewing the maximum quality video and picture content, please kindly hunt and find more informative video content and images that fit your interests.
Proof By Induction Examples. The symbol P denotes a sum over its argument for each natural. 123n1n Xn i1 i. Let a n be the sequence de ned by a 1 1 a 2 8 and a n a n 1 2a n 2 for n 3. Let k 2Z be given and suppose is true.
Mathematical Induction Proof For The Sum Of Squares Mathematical Induction Sum Of Squares Math Videos From pinterest.com
Prove that a n 3 2n 1 2 1n for all n 2N. When n 1 the left side of is 1 and the right side is 11 12 1 so both sides are equal and holds for n 1. Return to the Lessons Index Do the Lessons in Order Print-friendly page. We will prove by induction that for all n 2Z Xn i1 f i f n2 1. 16 N 11 5A for some integer A. Provide a justification at each step of the proof and highlight which step makes use of the inductive hypothesis.
Some of the basic contents of a proof by.
These norms can never be ignored. Now suppose for some R1 ๐ 4 รก1is divisible by 3. When n 1 the left side of is a 1 1 and the right side is 3 20. The next step in mathematical induction is to go to the next element after k and show that to be true too. The principle of mathematical induction is used to prove that a given proposition formula equality inequality is true for all positive integer numbers greater than or equal to some integer N. While doing this we will also go through examples of how to write proof ideas and details as well as algorithm ideas and details which you will need to write in your homework solutions.
Source: cz.pinterest.com
Closing Statement this is crucial in gaining all the marks. Induction is really important so the best thing to understand induction is to do it yourselfOf course a few examples never hurt. This is the hypothesis. Return to the Lessons Index Do the Lessons in Order Print-friendly page. Start with some examples below to make sure you believe the claim.
Source: pinterest.com
Proof by Induction - Examp. Provide a justification at each step of the proof and highlight which step makes use of the inductive hypothesis. We review some examples of proof by induction. 3 k1 is also 33 k. This is the hypothesis.
Source: pinterest.com
The symbol P denotes a sum over its argument for each natural. Assume statement is true for n k. Show it is true for the first one. For the base ๐1413 which is divisible by 3. While writing a proof by induction there are certain fundamental terms and mathematical jargon which must be used as well as a certain format which has to be followed.
Source: pinterest.com
Whether the proof uses weak induction or strong induction. 23n 2 n for all n 3. We will use proof by induction to show that 16 N 11 is divisible by 5. 123n1n Xn i1 i. Worked examples page 3 of 3 Sections.
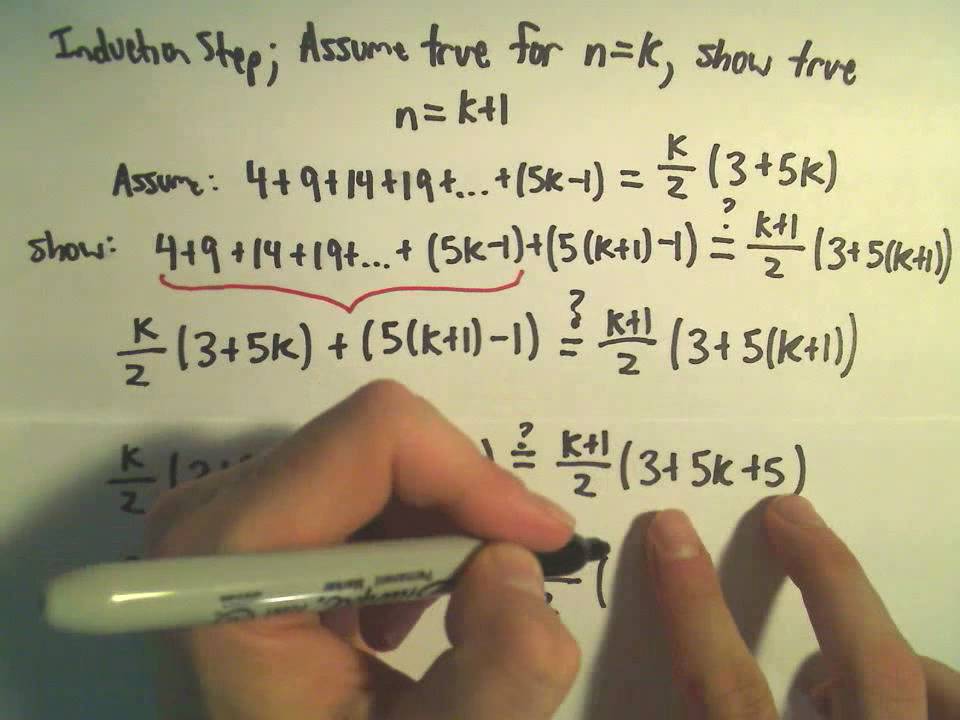Source: pinterest.com
Return to the Lessons Index Do the Lessons in Order Print-friendly page. Show it is true for the first one. Let us denote the proposition in question by P n where n is a positive integer. Proof by induction involves statements which depend on the natural numbers n 123. Let k2N be given and suppose formula holds for n k.
Source: pinterest.com
Induction is really important so the best thing to understand induction is to do it yourselfOf course a few examples never hurt. If you can do that you have used mathematical induction to prove that the property P is true for any element and therefore every element in the infinite set. 3 k1 is also 33 k. Provide an example of a proof by mathematical induction. Induction Proofs III Sample Proofs AJ.
Source: pinterest.com
Start with some examples below to make sure you believe the claim. So we have used proof by induction to show that 1 2. Show conjecture is true for n k 1. There are four basic proof techniques to prove p q where p is the hypothesis or set of hypotheses and q is the result. Return to the Lessons Index Do the Lessons in Order Print-friendly page.
Source: pinterest.com
Uses worked examples to demonstrate the technique of doing an induction proof. Now suppose for some R1 ๐ 4 รก1is divisible by 3. Basic Examples A sample induction proof We will prove by induction that for all n2N Xn i1 i nn 1 2. The next step in mathematical induction is to go to the next element after k and show that to be true too. So we have used proof by induction to show that 1 2.
Source: pinterest.com
Return to the Lessons Index Do the Lessons in Order Print-friendly page. Let k2N be given and suppose formula holds for n k. Worked examples page 3 of 3 Sections. The next step in mathematical induction is to go to the next element after k and show that to be true too. The 3k1 in this case is often helpful when doing proofs by induction on inequalities.
Source: pinterest.com
We will prove by strong induction that for all n 2N a n 3 2n 1 2 1n. Induction is really important so the best thing to understand induction is to do it yourselfOf course a few examples never hurt. While doing this we will also go through examples of how to write proof ideas and details as well as algorithm ideas and details which you will need to write in your homework solutions. We write the sum of the natural numbers up to a value n as. Introduction Examples of where induction fails Worked examples For n 1 2 2 2.
Source: pinterest.com
When n 1 the left side of is 1 and the right side is 11 12 1 so both sides are equal and holds for n 1. Sample strong induction proof. Induction Proofs III Sample Proofs AJ. We start with the base case. 2 Proof by induction Assume that we want to prove a property of the integers Pn.
Source: pinterest.com
January 17 2021 - Watch Video In addition to such techniques as direct proof proof by contraposition proof by contradiction and proof by cases there is a fifth technique that is quite useful in proving quantified statements. Uses worked examples to demonstrate the technique of doing an induction proof. Induction Proofs III Sample Proofs AJ. You have proven mathematically that everyone in the world loves puppies. We will prove by strong induction that for all n 2N a n 3 2n 1 2 1n.
Source: pinterest.com
2 Proof by induction Assume that we want to prove a property of the integers Pn. And then split 3. 16 N 11 5A for some integer A. Let us denote the proposition in question by P n where n is a positive integer. We will use proof by induction to show that 16 N 11 is divisible by 5.
Source: pinterest.com
A proof by induction proceeds as follows. A proof by induction proceeds as follows. Use induction to prove that all integers of the type ๐ 4 รก1 are divisible by 3 for all integers R1. Provide a justification at each step of the proof and highlight which step makes use of the inductive hypothesis. Show conjecture is true for n 1 or the first value n can take STEP 2.
Source: pinterest.com
Proof By Induction w 9 Step-by-Step Examples. We write the sum of the natural numbers up to a value n as. Basic Examples A sample induction proof We will prove by induction that for all n2N Xn i1 i nn 1 2. When n 1 the left side of is 1 and the right side is 11 12 1 so both sides are equal and holds for n 1. We will prove by induction that for all n 2Z Xn i1 f i f n2 1.
Source: pinterest.com
Now suppose for some R1 ๐ 4 รก1is divisible by 3. We write the sum of the natural numbers up to a value n as. Provide an example of a proof by mathematical induction. You da real mvps. Show it is true for the first one.
Source: pinterest.com
A proof by induction proceeds as follows. The symbol P denotes a sum over its argument for each natural. You da real mvps. For the base ๐1413 which is divisible by 3. Proof by Induction - Examp.
Source: pinterest.com
Worked examples page 3 of 3 Sections. 16 N 11 5A for some integer A. You have proven mathematically that everyone in the world loves puppies. We will prove by induction that for all n 2Z Xn i1 f i f n2 1. Some of the basic contents of a proof by.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title proof by induction examples by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
