Your Maximum likelihood estimation example images are ready in this website. Maximum likelihood estimation example are a topic that is being searched for and liked by netizens today. You can Download the Maximum likelihood estimation example files here. Get all royalty-free photos.
If you’re searching for maximum likelihood estimation example pictures information connected with to the maximum likelihood estimation example keyword, you have pay a visit to the right blog. Our site frequently provides you with suggestions for seeking the highest quality video and picture content, please kindly hunt and locate more informative video content and graphics that fit your interests.
Maximum Likelihood Estimation Example. MIT RES6-012 Introduction to Probability Spring 2018View the complete course. For example if is a parameter for the variance and ˆ is the maximum likelihood estimate for the variance then p ˆ is the maximum likelihood estimate for the standard deviation. Then we will calculate some examples of maximum likelihood estimation. We will see this in more detail in what follows.
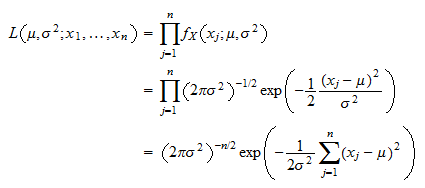Normal Distribution Maximum Likelihood Estimation From statlect.com
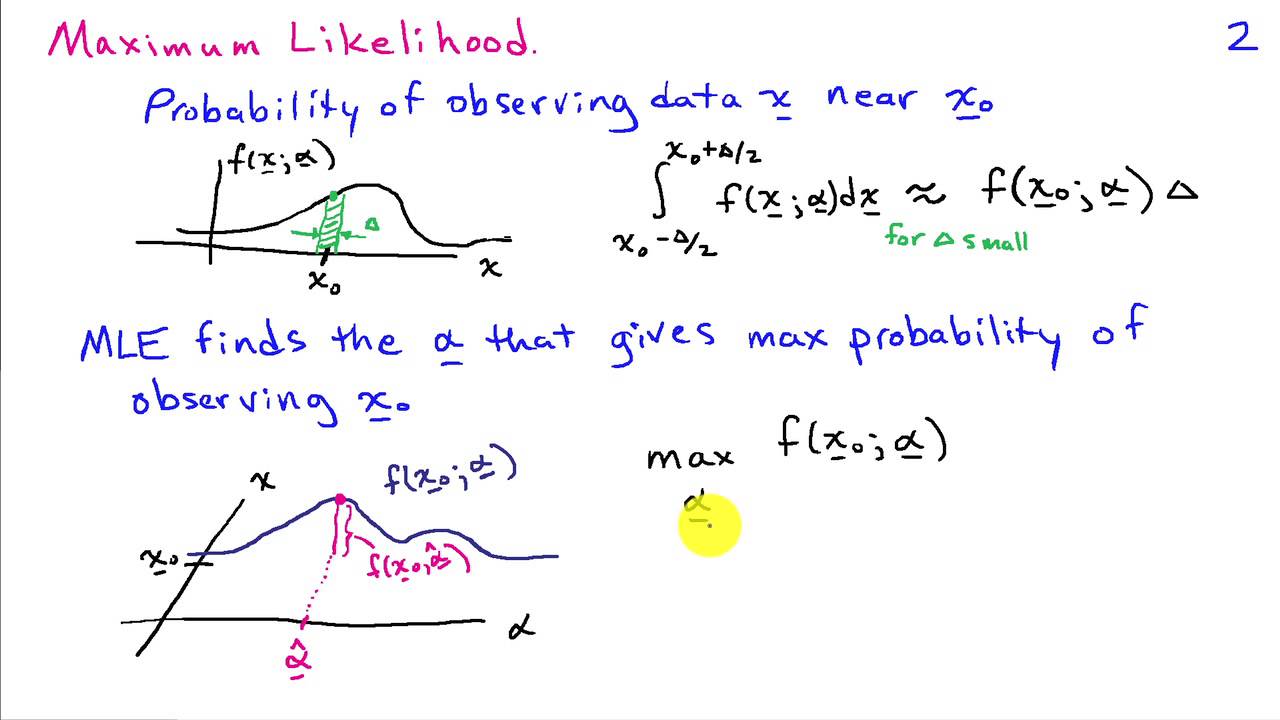
Based on the definitions given above identify the likelihood function and the maximum likelihood estimator of mu the mean weight of all American female college students. When we find the maximum of the likelihood function we actually find the parameters which are most likely to have. As said before the maximum likelihood estimation is a method that determines values for the parameters of a model. With prior assumption or knowledge about the data distribution Maximum Likelihood Estimation helps find the most likely-to-occur distribution. Starting with the first step. Maximum likelihood estimation can be applied to a vector valued parameter.
The following example illustrates how we can use the method of maximum likelihood to estimate multiple parameters at once.
As said before the maximum likelihood estimation is a method that determines values for the parameters of a model. Examples of Maximum Likelihood Estimation and Optimization in R Joel S Steele Univariateexample Hereweseehowtheparametersofafunctioncanbeminimizedusingtheoptim. This three-dimensional plot represents the likelihood function. Then we will calculate some examples of maximum likelihood estimation. The method of maximum likelihood uses the likelihood function to find point estimators by taking the derivative of the likelihood function with respect to θ setting it equal to zero and solving. Those parameters are found such that they maximize the likelihood function.
Source: youtube.com
Example 428 Let X be a single observation taking values from f012gaccording to Pq where q q0 or q1 and the values of Pq j fig are. Where the constant at the beginning is ignored. In this case the maximum likelihood estimator is also unbiased. In both cases the maximum likelihood estimate of theta is the value that maximizes the likelihood function. Songfeng Zheng 1 Maximum Likelihood Estimation Maximum likelihood is a relatively simple method of constructing an estimator for an un-known parameter µ.
Source: slideserve.com
We do this in such a way to maximize an associated joint probability density function or probability mass function. Those parameters are found such that they maximize the likelihood function. Maximum likelihood estimation can be applied to a vector valued parameter. Maximum likelihood estimation MLE is a technique used for estimating the parameters of a given distribution using some observed data. The basic idea behind maximum likelihood estimation is that we determine the values of these unknown parameters.
Source: stackoverflow.com
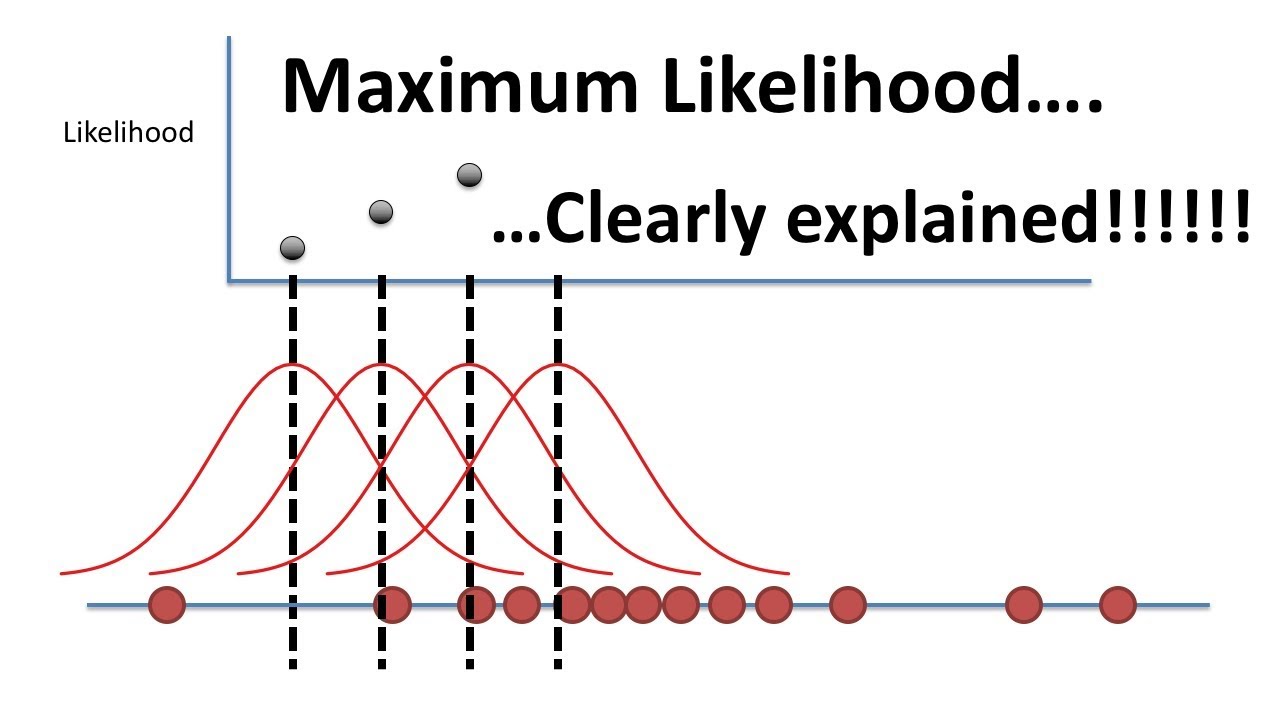
Likelihood. Two penalties are possible with the function. The following example illustrates how we can use the method of maximum likelihood to estimate multiple parameters at once. With prior assumption or knowledge about the data distribution Maximum Likelihood Estimation helps find the most likely-to-occur distribution. A look at the likelihood function surface plot in the figure below reveals that both of these values are the maximum values of the function.
Source: youtube.com
The values that we find are called the maximum likelihood estimates MLE. In both cases the maximum likelihood estimate of theta is the value that maximizes the likelihood function. To this end Maximum Likelihood Estimation simply known as MLE is a traditional probabilistic approach that can be applied to data belonging to any distribution ie Normal Poisson Bernoulli etc. 15 - Maximum-likelihood ML Estimation. Likelihood.
Source: youtube.com
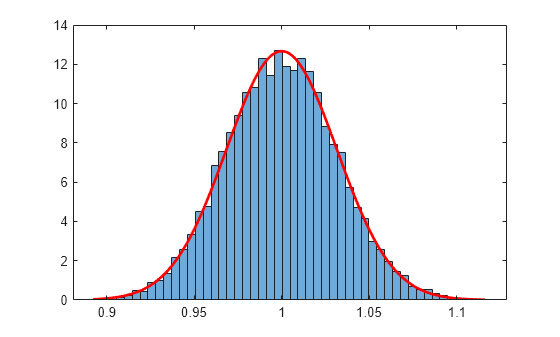
Example 4 Normal data. Find the maximum likelihood estimate for the pair 2. Likelihood and maximum likelihood estimator MLE The maximum likelihood method is the most popular method for deriving estimators in statistical inference that does not use any loss function. Check that this is a maximum. When we find the maximum of the likelihood function we actually find the parameters which are most likely to have.
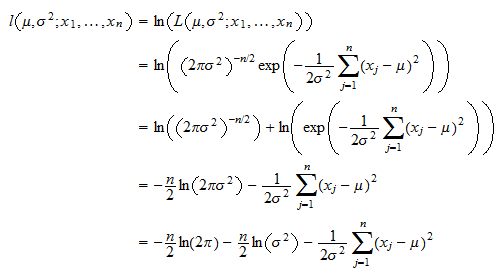Source: statlect.com
The method of maximum likelihood uses the likelihood function to find point estimators by taking the derivative of the likelihood function with respect to θ setting it equal to zero and solving. A look at the likelihood function surface plot in the figure below reveals that both of these values are the maximum values of the function. Normal distributions Suppose the data x 1x 2x n is drawn from a N 2 distribution where and are unknown. The Maximum Likelihood Estimator We start this chapter with a few quirky examples based on estimators we are already familiar with and then we consider classical maximum likelihood estimation. Those parameters are found such that they maximize the likelihood function.
Source: stats.stackexchange.com
The values that we find are called the maximum likelihood estimates MLE. The method of maximum likelihood uses the likelihood function to find point estimators by taking the derivative of the likelihood function with respect to θ setting it equal to zero and solving. As can be seen from the plot the maximum likelihood estimates for the two parameters correspond with the peak or maximum of the likelihood. Thus px x. For example if is a parameter for the variance and ˆ is the maximum likelihood estimate for the variance then p ˆ is the maximum likelihood estimate for the standard deviation.
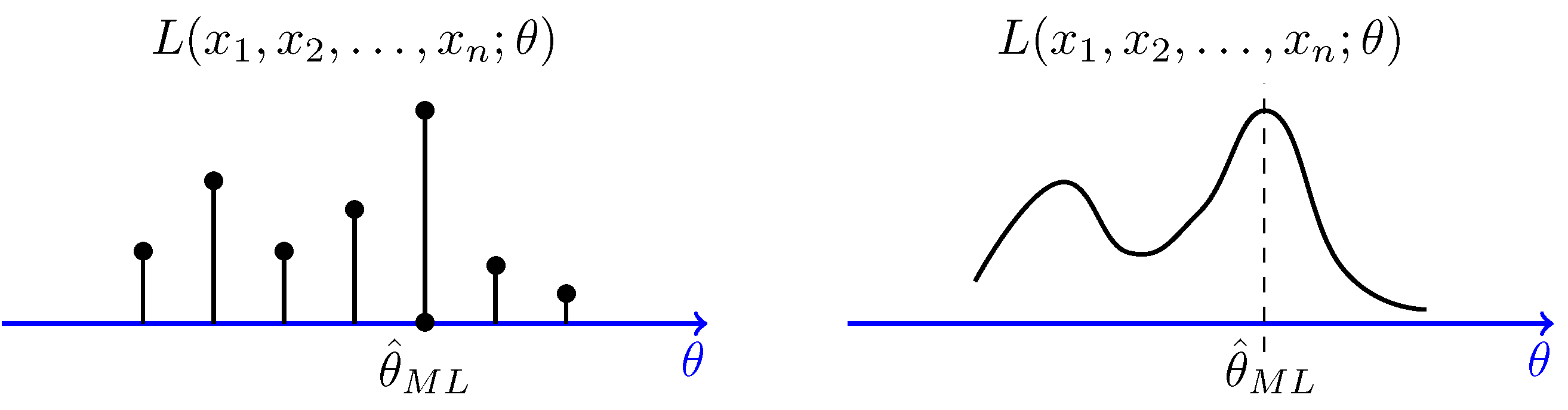Source: probabilitycourse.com
Those parameters are found such that they maximize the likelihood function. Examples of Maximum Likelihood Estimation MLE Part A. Define a function that will calculate the likelihood function for a given value of p. When we find the maximum of the likelihood function we actually find the parameters which are most likely to have. A graph of L p.
Source: youtube.com
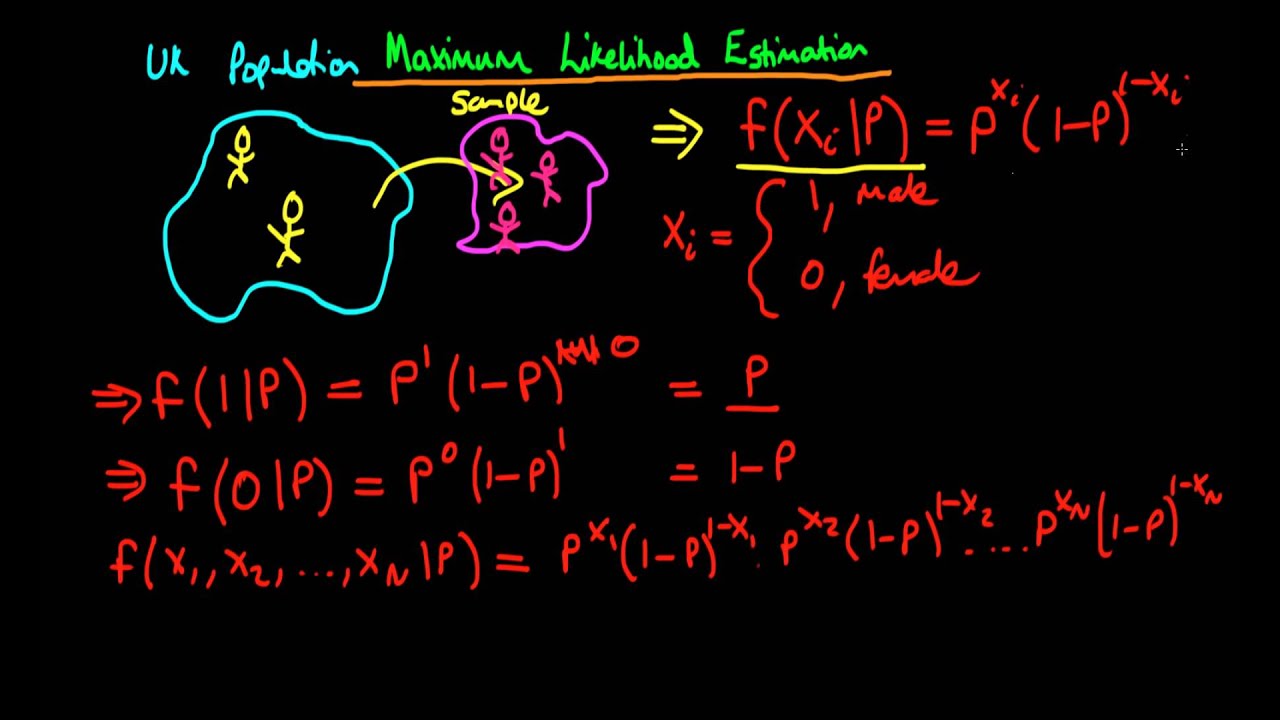
Define a function that will calculate the likelihood function for a given value of p. In the second one theta is a continuous-valued parameter such as the ones in Example 88. If the outcome is X 3 the likelihood is. In this case the maximum likelihood estimator is also unbiased. The purple coin is slightly weighted to land tails up about 60 of flips.
Source: mathworks.com
Now that we have an intuitive understanding of what maximum likelihood estimation is we can move on to learning how to calculate the parameter values. In this bag I have two coins. Using the given sample find a maximum likelihood estimate of mu as well. Let X be the total number of successes in the trials so that X B i n 5 p. Introduction to Maximum Likelihood Estimation Eric Zivot July 26 2012.
Source: stackoverflow.com
A look at the likelihood function surface plot in the figure below reveals that both of these values are the maximum values of the function. Maximum likelihood estimation can be applied to a vector valued parameter. This demonstration regards a standard regression model via penalized likelihood. See the Maximum Likelihood chapter for a starting point. Figure 81 - The maximum likelihood estimate for theta.
Source: youtube.com
Likelihood. Fisher a great English mathematical statis-tician in 1912. Example 428 Let X be a single observation taking values from f012gaccording to Pq where q q0 or q1 and the values of Pq j fig are. See the Maximum Likelihood chapter for a starting point. The basic idea behind maximum likelihood estimation is that we determine the values of these unknown parameters.
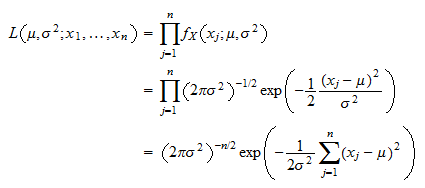Source: statlect.com
Check that this is a maximum. Based on the definitions given above identify the likelihood function and the maximum likelihood estimator of mu the mean weight of all American female college students. Suppose that an experiment consists of n 5 independent Bernoulli trials each having probability of success p. Example 3 Bernoulli example continued Given the likelihood function. Find the maximum likelihood estimate for the pair 2.
Source: medium.com
Check that this is a maximum. In many cases it can be shown that maximum likelihood estimator is the best estimator among all. The Maximum Likelihood Estimator We start this chapter with a few quirky examples based on estimators we are already familiar with and then we consider classical maximum likelihood estimation. As said before the maximum likelihood estimation is a method that determines values for the parameters of a model. Examples of Maximum Likelihood Estimation and Optimization in R Joel S Steele Univariateexample Hereweseehowtheparametersofafunctioncanbeminimizedusingtheoptim.
Source: researchgate.net
We will see this in more detail in what follows. As can be seen from the plot the maximum likelihood estimates for the two parameters correspond with the peak or maximum of the likelihood. Examples of Maximum Likelihood Estimation MLE Part A. Starting with the first step. Here the penalty is specified via lambda argument but one would typically estimate the model via cross-validation or some other fashion.
Source: youtube.com
Lets play a game. Again well demonstrate this with an example. Suppose that an experiment consists of n 5 independent Bernoulli trials each having probability of success p. Those parameters are found such that they maximize the likelihood function. A graph of L p.
Source: slideplayer.com
As can be seen from the plot the maximum likelihood estimates for the two parameters correspond with the peak or maximum of the likelihood. The values that we find are called the maximum likelihood estimates MLE. In this case the maximum likelihood estimator is also unbiased. Starting with the first step. If the outcome is X 3 the likelihood is.
Source: researchgate.net
One is painted green the other purple and both are weighted funny. In the second one theta is a continuous-valued parameter such as the ones in Example 88. Where the constant at the beginning is ignored. Normal distributions Suppose the data x 1x 2x n is drawn from a N 2 distribution where and are unknown. Find the maximum likelihood estimate for the pair 2.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site helpful, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title maximum likelihood estimation example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
